

Ultimately chess is just chess – not the best thing in the world and not the worst thing in the world, but there is nothing quite like it. – W.C. Fields

If you are a parent of small children – like myself – the following type of dialogue may sound familiar to you:
Your child: Why can I have only one glass of apple juice?
You: Because we will eat dinner soon, I don’t
want you to spoil your appetite!
Your child: Why does apple juice spoil my appetite?
You: Because it's filling and it has a lot of
sugar!
Your child: Why can't I have sugar?
You: Because it will make you more thirsty and
it's not good for your teeth!
Your child: Why is sugar not good for my teeth?
You: Eating sugar attracts bacteria and they
make holes in your teeth!
Your child: Why do bacteria make holes in my teeth?
At this point some things may run out, such as your patience, and possibly you ask yourself if this will ever end. A good question. Indeed, logically it may not end: Start with any question. And after every answer “Because….” simply ask “Why?”. In this fashion, a trilemma is created, a dilemma with three rather than merely two unsatisfactory alternatives. The philosophers call this particular one the Muenchhausen trilemma. These are the three alternatives:
In mathematics, for example, the third option is chosen. One starts to build a theory from a set of so called axioms, i.e. truths that one places at the beginning, which one cannot prove but takes as self-evident. Then from these initial truths further truths are derived: New knowledge follows from old knowledge through the application of logical arguments (rules of inference such as modus ponens). Famous in mathematics are the axioms of Euclid with which he began his epic studies of geometry, such as his Axiom 1: “For each pair of distinct points there is a unique line that passes through these points.”
All three of the mentioned alternatives are intellectually unsatisfactory. And in view of this trilemma, life is somewhat incomplete.We can never logically assert something.
Chess is a self-contained universe of 64 squares with 32 pieces and certain well-defined laws of motion. Is it possible to assert or prove something in chess? For example the simple statement: “In a certain position, White is better.”
One could try to reason like this: If White plays a certain move, then Black is worse. Why is Black worse? Because after any Black move, White is always better. Why is White always better? Because after any Black move, White has a move after which Black ist worse…. Looks like an infinite regress here also, just as the one we encountered before.
But a closer look shows that this is not the case. There is no Muenchhausen trilemma in chess. In principle, there are definite truths in chess, and here is how to see why.
Change the perspective for a moment and start at the very end of the game: consider a database with all positions in which Black is mated. It contains only a finite number of positions. Then consider a second database connected to the first one. This second database contains all positions in which White can give mate in one move. Then a third database connected to the second in which Black to move cannot defend against White mating him in 1, and so on. Always one half move further away from mate. One can – in principle – continue this process sequentially up to positions with all 32 pieces and White to move. Then the set W of all these 32-piece positions is connected through the shortest path in this sequence of databases to a mate position. Starting from one of these 32-piece positions, the corresponding path shows the moves for perfect play by both sides. If it is Black's move, there is no other defence that can delay his being mated longer. If it is White's move there is no alternative that gives him a faster mate. The set W hence contains all positions in which White can force a win.
Something analogous can be done from Black's perspective, starting with a database of all positions, in which White is mated. Continuing similarly as above, one gets a set B of 32-piece positions in which, with White to move, Black has a forced win. All other 32-piece positions, i.e. all except those in the sets W and B, make up a set D and lead to a draw with best play on both sides.
As a result, one can envision a database containing all legal positions and with a unique verdict being attached to each one of them: +1, ±0, –1 denoting White wins, draw, Black wins. So, in principle, we have designed an algorithm to construct perfect play in chess. Of course, in practice this is utopic for the full set of 32-piece positions. Not anymore though for six-piece endgames and even for some seven-piece endgames. But more importantly while objective truth is impossible in life, it is, in general, possible in chess. In this sense, chess is more complete than life.
Still even in chess there are curiosities attached to the theme of this note. Consider for example the following position from a discussion related to quantum logic in chess:
Vasilenko and Frolkin, 1995
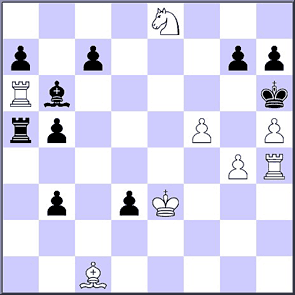
Mate in two moves
(a) Diagram
(b) After the first two half moves
(c) Before the last two half moves
If you have a position with the stipulation “White mates in n moves” and you play two half moves, namely the best white move and the best black response, then you should obtain a position on which you can put the stipulation “White mates in n–1 moves”. But this is not the case in the above problem.
Similarly, if from the starting position you go back two half moves, taking back the last black move (if there is a unique one) and after that the last white move (again if there is a unique one) then you should arrive at a position on which you can pin the stipulation “White mates in n+1 moves.” This, also, is not the case in the above problem.
In fact in all three positions (a), (b), (c), no matter whether you rewind by two half moves or move forward by two half moves from the above diagram, you still arrive at positions with the stipulation “White mates in 2”. A case of some very unusual arithmetic on the chess board: 2–1=2 and 2+1=2. And a fascinating example where two positions which differ by a legal move have a logically different future.
Can you find the solution in each of the three cases?
Hint: Remember the convention used in chess problems that an en passant capture is only permissible if it can be proven that the last move prior to the diagram position was the double-step of the pawn to be captured.
The solution to this problem will be provided in the next installment.
 About
the author
About
the authorChristian Hesse holds a Ph.D. from Harvard University and was on the faculty of the University of California at Berkeley until 1991. Since then he is Professor of Mathematics at the University of Stuttgart (Germany). Subsequently he has been a visiting researcher and invited lecturer at universities around the world, ranging from the Australian National University, Canberra, to the University of Concepcion, Chile. Recently he authored “Expeditionen in die Schachwelt” (Expeditions into the world of chess, ISBN 3-935748-14-0), a collection of about 100 essays that the Viennese newspaper Der Standard called “one of the most intellectually scintillating and recommendable books on chess ever written.”
Christian Hesse is married, has a six-year-old daughter and a two-year-old son. He lives in Mannheim and likes Voltaire's reply to the complaint: ”Life is hard” – “Compared to what?”.