Chess Expeditions
By Prof. Christian Hesse

Ultimately chess is just chess - not the best thing in the world
and not the worst thing in the world, but there is nothing quite like it.
– W.C. Fields
A Mathematical Chessboard Paradox
The Federal Ministry of Science and Research in Germany had proclaimed 2008
the “Year of Mathematics”. In addition, in 2008 both a Chess World Championship
and a Chess Olympiade took place, so that one may also think of 2008 as the
“Year of Chess”. This provides more than enough reason to look at an interesting
problem at the interface of these two intellectual activities: mathematics and
chess. It is a fascinating paradox which seems to prove that 64 is equal to
65 simply by cutting a chessboard (which, of course, consists of 64 squares)
into four pieces and by assembling these pieces into a rectangle whose sides
are made up of 5 squares and 13 squares, respectively (which, of course, results
in an area of 5 . 13 = 65 squares).
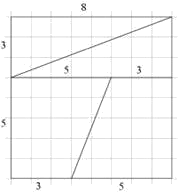
Specifically, what I have in mind is this:
With three straight cuts the chessboard has been dissected into two equal triangles
and two equal trapezoids. The sum of the areas of these four pieces is 64 little
squares of the chessboard. These four geometric pieces of the chessboard dissection
may now be reassembled into the following rectangle.
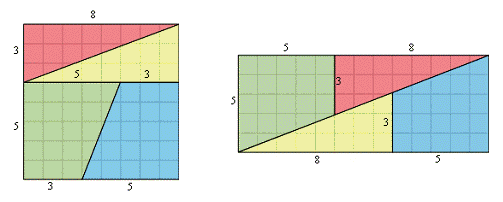
Please compare each of the four pieces in the two diagramms. The sides of the
resulting rectangle are made up of 5 and (8+5) = 13 little squares. Hence the
area of the rectangle is 5 x 13 = 65. These are the same four pieces as cut
out from the chessboard, only arranged differently. Hence their total area must
also be the same.
Therefore, we have proved that 64 = 65! Obviously, this is not true and there
must be a mistake somewhere. Can you find it?
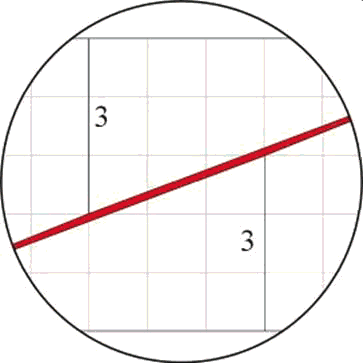
What lies at the center of the above paradox are drawing inaccuracies of the
lines that make up the triangles and the trapezoids and hence the rectangle.
Drawn at a higher resolution, the above diagramm should look like this:
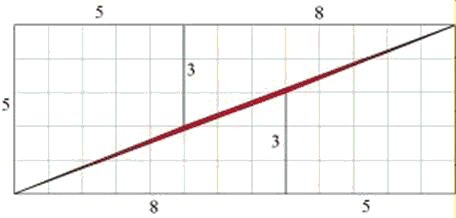
And zooming in on the central area one sees the rift between upper and lower
parts even more clearly:
The area highlighted in red in the above diagramms has the shape of a very
long parallelogram. It is responsible for the difference in area between the
square and the rectangle.
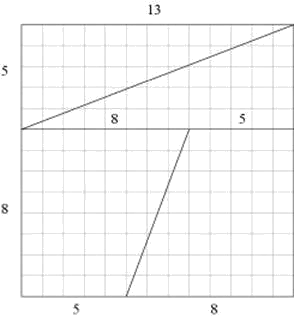
A similar dissection paradox can be constructed when starting with a 13x13-square
and rearranging the two triangles and two trapezoids that make it up into a
21x8-rectangle in a similar fashion as above:
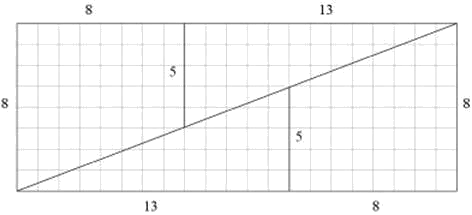
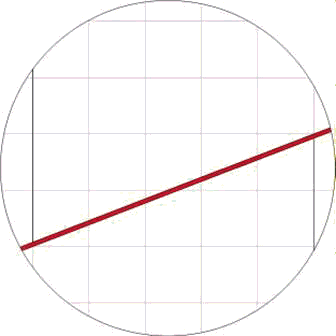
Again at a higher resolution we have:
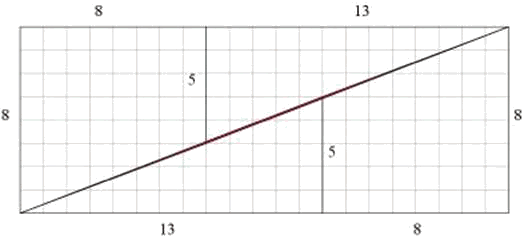
The area colored in red is again a parallelogram of area 1 where this time
the upper and lower parts do overlap. Hence in this case, there is no rift here,
but the resulting rectangle has a smaller area (=168) than the original square
(=169) due to the overlapping.
What is the mathematical core of this paradox? To explain it in general, we
start by mentioning the sequence of so called Fibonacci numbers Fn.
This is a sequence of numbers in which each following number Fn+1
is defined as the sum of the two immediately preceeding numbers Fn
and Fn-1. Hence:
Fn+1 = Fn + Fn-1 for all n = 1, 2, 3, …
The starting values are given by F0 = 0 and F1 = 1. Thus
the first few values of the Fibonacci sequence are
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
The above dissection paradox then seems to say that
Fn . Fn equals Fn+1 .
Fn-1
Let us perform some simple calculations to see what is really
going on:
Fn . Fn = Fn(Fn-1
+ Fn-2) = Fn . Fn-1 + Fn
. Fn-2
and
Fn+1
. Fn-1 = (Fn + Fn-1)Fn-1
= Fn . Fn-1 + Fn-1 .
Fn-1
The difference Dn
between these two products is:
Dn =
Fn+1 . Fn-1 - Fn .
Fn
=
Fn-1 . Fn-1 - Fn
. Fn-2
=
-Dn-1 = (-1)2 Dn-2 = ... = (-1)n-1D1
= (-1)n
since D1
= F2 . F0 – F1 . F1
= 1 . 0 – 1 . 1 = (-1)1.
Therefore we have
established the truth of what is known as Cassini`s identity:
Fn+1
. Fn-1– Fn . Fn =
(-1)n
The conclusion is:
One can always reorganize an Fn x Fn -square into an Fn+1
x Fn-1 -rectangle and the difference between their areas, namely
Fn . Fn and Fn+1 . Fn-1
respectively, is (-1)n , i.e. either -1 or +1. In the first case,
one has an overlap between the pieces. In the second case, there is a rift between
them.
The next largest square
for which the dissection works is a 21x21-square which in the above fashion
may be reorganized into a 34x13-rectangle. You may work out how the 21x21-square
needs to be cut by simply thinking of the Fibonacci sequence.
 About
the author About
the author
Christian Hesse holds a Ph.D. from Harvard University and was on the
faculty of the University of California at Berkeley until 1991. Since
then he is Professor of Mathematics at the University of Stuttgart (Germany).
Subsequently he has been a visiting researcher and invited lecturer at
universities around the world, ranging from the Australian National University,
Canberra, to the University of Concepcion, Chile.
Recently he authored “Expeditionen
in die Schachwelt” (Expeditions into the world of chess, ISBN
3-935748-14-0), a collection of about 100 essays that the Viennese newspaper
Der Standard called “one of the most intellectually scintillating
and recommendable books on chess ever written.”
Christian Hesse is married, has an eight-year-old daughter and a four-year-old
son. He lives in Mannheim and likes Voltaire's reply to the complaint:
”Life is hard” – “Compared to what?”.
|
Previous articles for ChessBase:























 About
the author
About
the author




